近日,国际通用工程学院/国际交叉科学研究院大二本科生丁屹达、Sebastian Wandelt教授、孙小倩副教授在交通领域知名期刊《Transportation Research Part C : Emerging Technologies》(影响因子6.077)上发表论文TLQP: Early-stage Transportation Lock-down and Quarantine Problem,以新冠疫情为研究背景,利用全球航空交通网络及疫情传播模型,研究能够有效遏制疫情发展、具有较低社会经济成本的防疫策略。
当今高密度、大流量的交通运输系统,尤其是占据主导地位的航空交通系统,使得一场地区性流行病愈加可能演变为全球大流行。除了保持社交距离和佩戴口罩,限制人员流动(如限制交通流量和封城)是一项必要的防疫措施。考虑到防疫措施相应的社会经济成本,关于限制交通流量和封城的决策可建模为组合最优化问题。本文提出了疫情初期削减交通流量及封城问题(TLQP: Early-stage Transportation Lock-down and Quarantine Problem),由此帮助决策者制定理论上最优的防疫策略。该决策建议框架以SEIR传染病模型及航空交通网络为载体,考量削减国际交通流量、削减国内交通流量及限制地区内部人口流动(即封城)这三类措施的防疫效果及相应的社会经济成本,由此求解出理论上最优的防疫策略(即防疫措施的组合)。鉴于此组合最优化问题的高复杂度,文章提出了一种高效且可靠的启发式算法(TLQP-H),以疫情传播有效距离(Effective Distance Path)和CELF算法(Cost-Effective Lazy Forward Algorithm)为基础。文章最后聚焦德国在2020年疫情的发展情况,分析德国在面对第一波及第二波全球疫情时理论上最优的防疫策略,为决策者提供有指导意义的防疫建议。
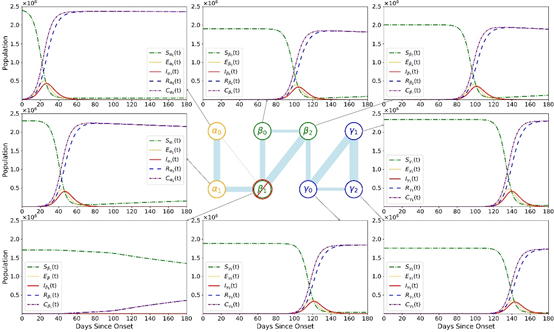
图1 疫情传播网络示意图及各节点的SEIR模型。该网络中,管理单元β 施加了两项防疫措施:削减90%的β1-α0的流量以及削减90%的β1的内部流量
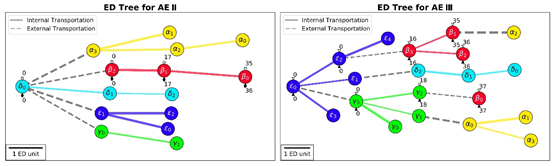
图2 疫情传播网络的有效距离树,节点间的链接宽度与流量呈正比,而长度(即有效距离)与流量呈负相关。
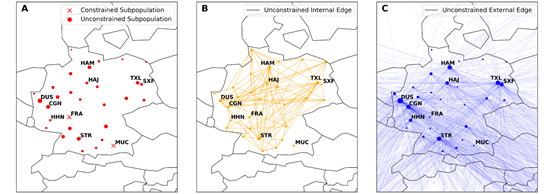
图3 TLQP-H模型模拟得出的在全球第一波疫情冲击下德国的理论最优防疫策略。图中的节点为以主要机场为中心的区域。图(A)中,“x”代表该节点施加了限制内部流量的措施,其他节点的大小与区域内人口数量成正比;图(B)、(C)中,显示的链接分别为未受限制的国内交通和国际交通,节点的大小代表了节点度。
国际通用工程学院/国际交叉科学研究院孙小倩副教授是论文的唯一通讯作者,她先后入选北航“卓越百人”和“青年拔尖”人才计划,德国亚琛工业大学冯卡门 Fellow,德累斯顿工业大学 Fellow,研究方向主要包括航空交通网络、多模式综合交通系统、大规模系统智能优化算法等。论文的第一作者是我校国际通用工程学院/国际交叉科学研究院大二本科生丁屹达,论文的合作者为北航电子信息工程学院Sebastian Wandelt教授。该项研究得到了国家自然科学基金的支持。
全文链接:https://www.sciencedirect.com/science/article/pii/S0968090X21002321








 北航校历
北航校历 校园地图
校园地图